Fr, 01.05.2015 - 11:02 — Peter Schuster 
![]() Bei Ausbruch einer Epidemie mit einem neuen Erreger besteht dringender Bedarf für ein mathematisches Modell, das den Verlauf der Epidemie möglichst verlässlich voraussagen kann, um darauf basierend effiziente Interventionen zum Schutz der Bevölkerung einzuleiten. Der theoretische Chemiker Peter Schuster erklärt, warum Prognosen, die auf in der Anfangsphase n einer Epidemie erhobenen Daten beruhen, wenig Aussagekraft für deren späten Verlauf haben [1].
Bei Ausbruch einer Epidemie mit einem neuen Erreger besteht dringender Bedarf für ein mathematisches Modell, das den Verlauf der Epidemie möglichst verlässlich voraussagen kann, um darauf basierend effiziente Interventionen zum Schutz der Bevölkerung einzuleiten. Der theoretische Chemiker Peter Schuster erklärt, warum Prognosen, die auf in der Anfangsphase n einer Epidemie erhobenen Daten beruhen, wenig Aussagekraft für deren späten Verlauf haben [1].
Lässt sich die Natur unter eine vollständige Kontrolle bringen? Am Beginn der zweiten Hälfte des 20. Jahrhunderts glaubten weite Kreise daran, dass die ungeheuren Fortschritte in den Naturwissenschaften und insbesondere in der Medizin dies erlauben würden. Es erschien absehbar, dass Gesundheitswesen und Pharmakologie bald in der Lage wären praktisch alle Krankheiten zu verhindern oder (zumindest) zu heilen. So war in den 1980er Jahren die Pharma-Industrie fest davon überzeugt diesem Ziel beispielsweise bei den Infektionskrankheiten sehr nahe gekommen zu sein. Man dachte ein mehr als ausreichendes Arsenal an Antibiotika zur Verfügung zu haben, um Infektionen aller Art (wenigstens in der „westlichen Welt“) erfolgreich bekämpfen zu können und stoppte die Suche nach neuen Antibiotika. Man löste also entsprechende Institutionen mitsamt ihrem Know-How und ihren Infrastrukturen auf und wandte sich anderen „erfolgversprechenderen“ Aufgaben zu. Wie sich bald zeigen sollte, war dies ein verhängnisvoller Irrtum:
Erstens, weil Mikroorganismen – Viren, Bakterien, Pilze und Protozoen - enorme Fähigkeiten besitzen, Resistenzen gegen Antibiotika zu entwickeln. Gegen die zunehmend resistent-werdenden Stämme werden heute neue Wirkstoffe dringendst benötigt!
Zweitens, weil Infektionskrankheiten aufgetaucht sind, die bis dahin völlig unbekannt waren oder zuvor nicht genügend Beachtung gefunden hatten. Es waren dies vor allem
- AIDS -das „acquired immunodeficiency syndrome“ (erworbenes Immunschwäche-Syndrom), das durch HIV - humane immunodeficiency virus – übertragen wird,
- Ebola, das vom Ebolavirus (EBOV - Ebola ist ein Fluss in der Republik Kongo, wo es 1976 den ersten Ausbruch dieser Infektion gab) und vier verwandten Stämmen von Filoviren übertragen wird,
- SARS – das schwere akute respiratorische Syndrom – verursacht von einem mutierten Coronavirus (SARS-CoV)
- die Tierseuche BSE (bovine spongiform encephalopathy) - Rinderwahn- , eine Epidemie in den 1990er-Jahren, die allerdings nicht durch ein Virus sondern Prionen (falschgefaltete infektiöse) Proteine ausgelöst wurde.
Diese und eine Reihe weiterer Epidemien haben die Welt in Angst und Schrecken versetzt. Es war ja keineswegs abzusehen, welchen Verlauf, welches Ausmaß diese neuen Infektionskrankheiten haben würden, wieweit man sie in Kontrolle bringen könnte oder ob sie in einer globalen Katastrophe enden würden.
Dringendst benötigt: verlässliche Modelle zur Prognose des Verlaufs von Epidemien
Wann immer eine Epidemie mit neuen Erregern ausbricht, ist es offensichtlich, dass ein dringender Bedarf für mathematische Modelle besteht, die den Verlauf derartiger neuer Seuchen simulieren und - darauf basierend - möglichst verlässlich voraussagen können. Dies gilt natürlich ebenso für schon besiegt geglaubte Infektionskrankheiten wie Keuchhusten und Masern, die als Folge der Impfgegner-Bewegung nun wieder aufgeflammt sind.
Verlässliche Prognosen sind unabdingbar, weil bereits beim Ausbruch einer Epidemie nur noch sehr wenig Zeit bleibt, um effiziente Interventionen zum Schutz der Bevölkerung und Strategien zur Behandlung der Erkrankten einzuleiten. Es sind dabei ja enorme logistische Herausforderungen zu bewältigen, die vom raschen Bereitstellen eines voraussichtlichen Bedarfs an Behandlungszentren, Labors, Spitalsbetten, Ärzten, Pflegekräften, Diagnostika und Therapeutika, etc. bis hin zu Restriktionen der Bewegungs- und Reisefreiheit reichen. Dazu kommen noch die dafür erforderlichen finanziellen Mittel.
Der Schrecken verbreitende Ausbruch von Ebola, der im Dezember 2013 in West-Afrika seinen Ausgang nahm und eine hohe Letalität verursachte, war Anlass eines Booms in epidemiologischen Modellierungen. Eine Reihe dieser Untersuchungen finden sich In dem neuen Fachjournal PLOS Currents: Outbreaks, das „open access“ ist. Die ersten Modellierungen stammen aus dem Herbst 2014, einer noch frühen Phase der Seuchenausbreitung. Nur drei Monate später war es aber klar, dass die Vorhersagen die Zahl der Infizierten und der Todesfälle um Größenordnungen überschätzt hatten. War man anfangs davon ausgegangen, dass es hunderttausende bis zu mehreren Millionen Infizierte und davon etwa 40 % Todesopfer geben könnte, so zeigte die Epidemie glücklicherweise einen wesentlich „leichteren“ Verlauf: laut aktuellen Daten der WHO sind bis jetzt weltweit 26 083 (bestätigte, wahrscheinliche und vermutete) Fälle von Ebola aufgetreten, davon 26 044 in den Staaten Guinea, Liberia und Sierra Leone, und 10 823 Todesfälle (davon 10 808 in den genannten drei Staaten). In allen drei Staaten treten nur mehr vereinzelte Infektionen auf [1]. (Abbildung 1).
Die Epidemie konnte also in den Griff bekommen werden. 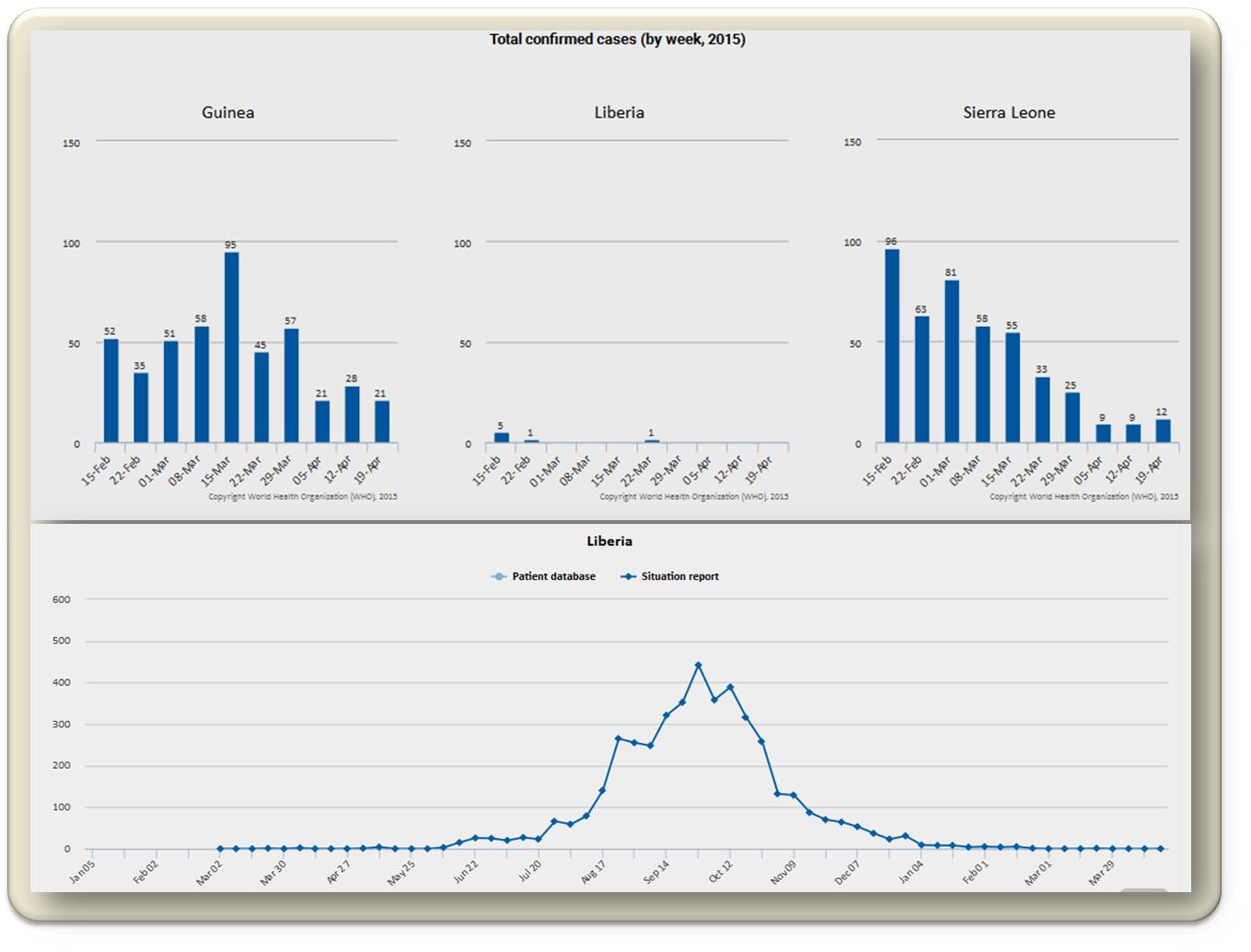 Abbildung 1. Verlauf der Ebola-Epidemie; oben: In den am stärksten betroffenen Staaten Guinea, Liberia und Sierra Leone vom 15.2, - 19.4.2015 und unten: Gesamtverlauf in Liberia vom Ausbruch der Epidemie bis jetzt. (Quelle: WHO)
Abbildung 1. Verlauf der Ebola-Epidemie; oben: In den am stärksten betroffenen Staaten Guinea, Liberia und Sierra Leone vom 15.2, - 19.4.2015 und unten: Gesamtverlauf in Liberia vom Ausbruch der Epidemie bis jetzt. (Quelle: WHO)
Wie können aber bessere epidemiologische Vorhersagen erstellt werden, wo weisen Modellierungen gravierende Fehler auf, wo können Fehler vermieden werden?
Dies soll im Folgenden an Hand des häufig verwendeten SEIR-Modells analysiert werden. Insbesondere die Frage nach der Aussagekraft der Prognosen, wenn aus den Anfangsphasen einer Epidemie auf deren späte Phasen extrapoliert wird.
Das SEIR Modell
ist ein relativ einfaches, sehr populäres mathematischen Modells, das den dynamischen Prozess simuliert, wie sich eine Infektion in einer Population aus anfänglich dafür anfälligen Individuen ausbreitet. Die Gesamtpopulation wird dabei aus vier Gruppen zusammengesetzt angenommen: aus Personen, i) die für die Infektion anfällig („susceptible“) sind , ii) die mit dem Erreger in Kontakt gekommen und infiziert aber noch symptomlos/nicht infektiös sind („exposed“), iii) die bereits die Krankheitssymptome zeigen und infektiös („infectious“) sind und iv)solchen, die entweder die Krankheit überstanden haben und nun immun sind oder daran verstarben („removed“). (Abbildung 2).
 Abbildung 2. Das SEIR Modell: Die vier Bevölkerungsgruppen und die 3 Prozesse, die den Verlauf der Epidemie beschreiben
Abbildung 2. Das SEIR Modell: Die vier Bevölkerungsgruppen und die 3 Prozesse, die den Verlauf der Epidemie beschreiben
Die Ausbreitung findet in drei aufeinanderfolgenden Schritten statt, die mit einfachen Gleichungen der chemischen Kinetik beschrieben werden können. Der Prozess beginnt mit einem (eingeschleppten) infizierten Individuum (I), das auf ein für die Infektion anfälliges Individuum (S) - trifft und dieses infiziert, wobei dieses noch symptomlos bleibt und auch nicht infektiös ist (E). Nach einer Latenzzeit wird E selbst infektiös (I), steckt andere an und wird im Krankheitsverlauf entweder wieder gesund oder stirbt (R).
Wie schnell sich die Epidemie nun ausbreitet, hängt einerseits von der sogenannten Basisreproduktionszahl und andererseits von der Generationszeit ab:
- Die Basisreproduktionszahl gibt an wie viele anfällige Personen eine infizierte Person ansteckt. Ist beispielweise die Basisreproduktionszahl 2, so steckt ein Infizierter 2 Anfällige an, diese nach der Latenzzeit insgesamt 4 Personen, in der nächsten Generation sind es 8, dann 16, dann 32, usw. Je höher die Basisreproduktionszahl ist, desto schneller breitet sich die Epidemie aus, je niedriger diese Zahl ist, desto langsamer ist sie. Im Verlauf dieses exponentiellen Wachstums nimmt die Zahl der infizierbaren Individuen laufend ab, damit sinkt die Reproduktionszahl. Kann ein Infizierter im Schnitt nur mehr eine Person anstecken, so steigt die Zahl der Infizierten nicht weiter, wird es weniger als 1 Person, erlischt die Krankheit.
- Die Generationszeit hängt von der Latenzzeit - der Zeitdauer zwischen Infektion und der Infektiosität – und der Dauer der Infektiosität ab.
Wie ein nach dem SEIR-Modell simulierter Verlauf einer Epidemie aussieht, ist in Abbildung 3 gezeigt. 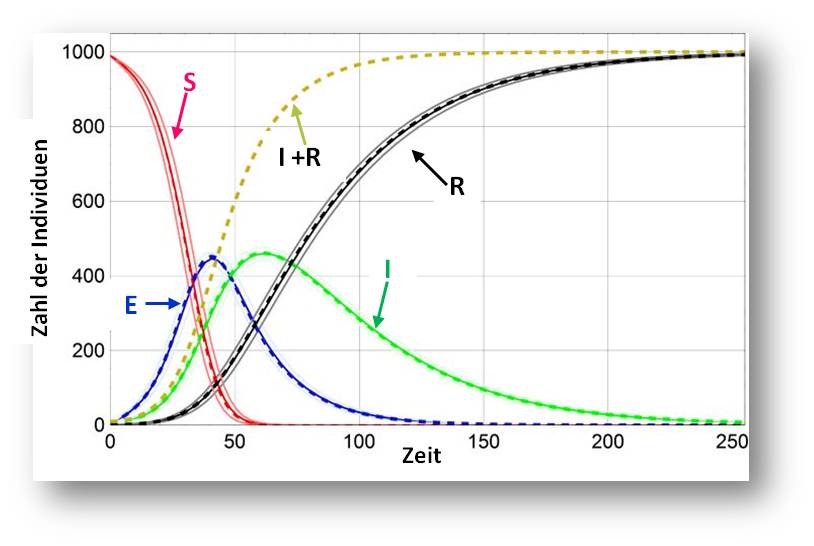
Abbildung 3.Nach dem SEIR-Modell berechnete Kurven für den Verlauf einer Epidemie. Annahme: anfangs gibt es 990 anfällige (R) und 10 infektiöse (I) Individuen und die Basisreproduktionszahl ist hoch (20).Die Kurven liegen in einem Band, das die Standardabweichungen anzeigt.
Warum weichen die Prognosen so stark von der Realität ab?
Das SEIR-Modell ist streng deterministisch, d.h.es gibt vor, dass mit entsprechend gut gewählten Parametern der Verlauf des Infektionsgeschehen realitätsnah simuliert und prognostiziert werden kann (in Abbildung 3 geben die stark eingezeichneten Kurven die Reaktionen (1) – (3) aus Abbildung 1 wider). Es wird damit eine idealisierte Situation beschrieben. Das Modell ignoriert ganz einfach Zufallsprozesse (stochastische Prozesse), wie sie durch variierende demographische Strukturen, räumliche Gegebenheiten und Umweltbedingungen gegeben sind. Stochastische Modelle, welche die Wahrscheinlichkeiten einzelner Vorgänge und Zustände berücksichtigen, sind daher, wann immer es möglich ist, vorzuziehen.
Ein ganz wesentliches Problem entsteht aber, wenn aus frühen Daten einer Epidemie auf deren Ausmaß in späten Phasen geschlossen werden soll. Wie bereits früher ausgeführt wurde, ist der Beginn einer Epidemie durch exponentielles Wachstum gekennzeichnet. Wenn nun die Infektion von wenigen Individuen (vielleicht auch nur von einem einzigen) ausgeht und die Zahl der anfälligen Individuen viel größer ist, ist es für die Anfangsphase unerheblich, wie viele diese sind. Die Ausbreitung wird in allen Fällen ununterscheidbar verlaufen (Abbildung 4) und damit keine Rückschlüsse auf die Zahl der Infizierten zu einem Zeitpunkt erlauben, wenn die Epidemie bereits unter Kontrolle ist.
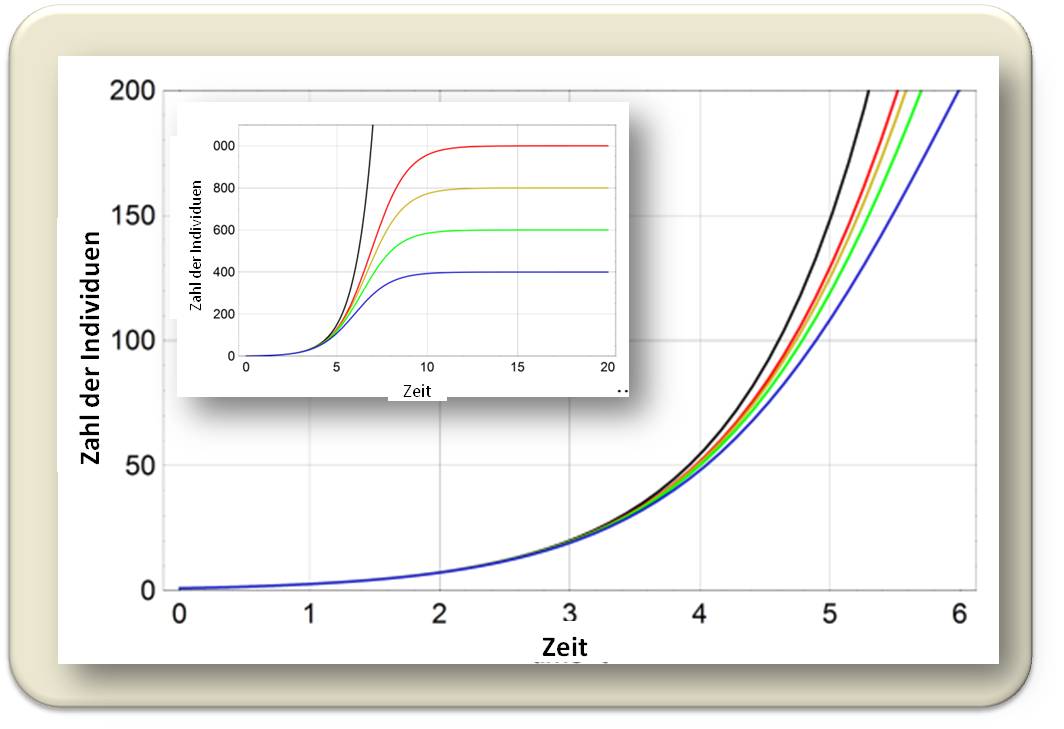 Abbildung 4. Anfänglich exponentielles Wachstum (großes Bild), das in eine Sättigung übergeht (Insert). Für das Wachstum in der Anfangsphase ist es unerheblich, wie viele infizierte Individuen es schlussendlich gibt. (Den Kurven liegt eine Gleichung von P.H, Verhulst zugrunde, der im Jahr 1838 damit ein vergleichbares Problem - das Wachstum einer sich vermehrenden Population bei limitierten Ressourcen - beschreibt.)
Abbildung 4. Anfänglich exponentielles Wachstum (großes Bild), das in eine Sättigung übergeht (Insert). Für das Wachstum in der Anfangsphase ist es unerheblich, wie viele infizierte Individuen es schlussendlich gibt. (Den Kurven liegt eine Gleichung von P.H, Verhulst zugrunde, der im Jahr 1838 damit ein vergleichbares Problem - das Wachstum einer sich vermehrenden Population bei limitierten Ressourcen - beschreibt.)
Dass dieses Problem nicht auf die Verbreitung von Epidemien beschränkt ist, demonstrieren beispielsweise die Voraussagen des berühmten Clubs of Rome; aus politischer Sicht waren diese vielleicht wünschenswert, wissenschaftlich aber völlig unhaltbar.
Ausblick
Der aktuelle Ausbruch von Ebola bietet theoretischen Epidemiologen ein sehr reiches Datenmaterial und damit eine einzigartige Gelegenheit vorhandene Modelle zu testen und verbesserte neue zu erstellen. Dabei sollte immer berücksichtigt werden, dass Daten, die in den frühen, exponentiell verlaufenden Phasen einer Epidemie erhoben werden, wenig Aussagekraft für deren späten Verlauf bieten können.
[1] Ein ausführlicher Artikel zu diesem Thema ist eben erschienen: Peter Schuster: Ebola – Challenge and revival of Theoretical Epidemiology. Why extrapolations from early phases of epidemics are problematic. Complexity (2015) DOI:10.1002/cplx
[2] WHO: Ebola in West Africa: 12-months on (14 Artikel)
Weiterführende Links
Bill Gates: The next epidemic – lessons from Ebola. N Engl J Med 2015; 372:1381-1384 April 9, 2015 DOI:10.1056/NEJMp1502918
Lars Schade (Robert Koch Institut, Deutschland) Ebola kompakt. Video 5:14 min. (16.7.2014)
Anita Schroven: Ebola-Epidemie - Liberia, Guinea, Sierra-Leone in der Krise Radiointerview 7:19 min (16.2.2015).
Infektionen jetten um die Welt. Video 5:56 min.
- Printer-friendly version
- Log in to post comments
