Recycling & Wachstum — Vom Ursprung des Lebens bis zur modernen Gesellschaft.
Recycling & Wachstum — Vom Ursprung des Lebens bis zur modernen Gesellschaft.Fr, 29.11.2013 - 08:56 — Peter Schuster
![]()
 Exponentielles Wachstum erschöpft sehr rasch und effizient die vorhandenen Ressourcen. Ist ein essentielles Reservoir entleert und eine Auffüllung nicht möglich, so stirbt die Mangel leidende Population aus. Dementsprechend liegt die einzige Möglichkeit mit raschem Wachstum zurecht zu kommen in der Wiederverwertung - dem Recyceln – von Material.
Exponentielles Wachstum erschöpft sehr rasch und effizient die vorhandenen Ressourcen. Ist ein essentielles Reservoir entleert und eine Auffüllung nicht möglich, so stirbt die Mangel leidende Population aus. Dementsprechend liegt die einzige Möglichkeit mit raschem Wachstum zurecht zu kommen in der Wiederverwertung - dem Recyceln – von Material.
Der britische Nationalökonom und Sozialphilosoph Robert Malthus (1766 - 1834) dürfte wohl der Erste gewesen sein, der sich mit den Konsequenzen auseinandersetzte, wenn Wachstum in Form einer geometrischen Progression* erfolgt. Konkret hatte er in einigen amerikanischen Kolonien, die über ausreichend Ressourcen verfügten, beobachtet, daß sich die Bevölkerung im Zeitabstand von jeweils 25 Jahren verdoppelte. In seinem „Essay on the Principle of Population” [1] stellte Malthus die These auf, dass sich die Population der Menschen in einer geometrischen Progression (1, 2, 4, 8, 16, 32, 64, 128…..) vermehrt, die Nahrungsmittelproduktion dagegen bestenfalls in arithmetischer Progression (linear; 1, 2, 3, 4, 5,6,…), dass es daher zu einer Auseinanderentwicklung von Lebensmittel-Nachfrage und Angebot kommen müsste. Als Konsequenz prognostizierte er eine steigende Verknappung der Lebensmittel, die zur fortschreitenden Verelendung der Bevölkerung, Hungersnöten, Krieg und Epidemien führen sollte.
Ununterbrochenes, grenzenloses Wachstum – eine Vervielfachung durch Autokatalyse* - wird heute üblicherweise durch eine Exponentialfunktion* dargestellt, wobei dafür auch unlimitierte Ressourcen angenommen werden. Eine klassische Veranschaulichung bedient sich der Metapher von den Seerosen: Angenommen, Seerosen verdoppeln täglich die Fläche, die sie auf einem Teich bedecken. Wenn sie vor drei Tagen ein Achtel des Teichs bedeckt hatten und damit kaum sichtbar waren, hatten sie sich vor zwei Tagen auf ein Viertel, vor einem Tag bereits auf die Hälfte des Teichs ausgedehnt und nehmen heute die gesamte Oberfläche ein – eine Katastrophe, da sie damit Licht abhängiges Leben im darunter liegenden Wasser verhindern.
Malthus hatte die einfache und nach wie vor gültige Voraussage gemacht, dass das Auseinanderdriften von Bevölkerungswachstum und Nahrungsmittelproduktion zu Hungerkatastrophen führen muss und nur durch Geburtenkontrolle in Schach gehalten werden kann (Abbildung 1).
 Abbildung 1. Essay on the Principle of Population. Robert Malthus veröffentlichte diese Abhandlung anonym im Jahre 1798 [1].
Abbildung 1. Essay on the Principle of Population. Robert Malthus veröffentlichte diese Abhandlung anonym im Jahre 1798 [1].
Auch, wenn neue Technologien, wie beispielsweise die „grüne Revolution“ der 1960er und 1970er Jahre, zu nicht vorhersehbaren Steigerungen der Ernteerträge führten, änderten diese nichts an dem prinzipiellen Problem:
Ein Mehr an verfügbarer Nahrung verursacht einen Anstieg in einer Population und zwar so lange, bis ein Grenzwert erreicht wird, an welchem die nun die vergrößerte Population zu hungern beginnt. Das Malthus-Modell zeigt Geburtenkontrolle als den einzig richtigen Ausweg aus dem Dilemma.
Wachstum und Biologische Evolution
Die biologische Evolution basiert darauf, dass sich die einzelnen Individuen in Populationen von Spezies multiplikativ vermehren und miteinander konkurrieren. Auch, wenn exponentielles Wachstum nur über eine limitierte Zeitspanne aufrecht erhalten werden kann, bleibt der Prozeß einer „Selection of the fittest“ der gleiche – ob es sich nun um eine wachsende, gleichbleibende oder sogar sinkende Population handelt, solange die Spezies nicht als Ganzes ausstirbt. Erfolgreiche Konkurrenz bei exponentiellem Wachstum gelingt nur Varianten, die exponentiell mit höherer Fitness oder solchen, die „hyperbolisch“ wachsen.
Abbildung 2 illustriert unterschiedliche Formen von Wachstumskurven
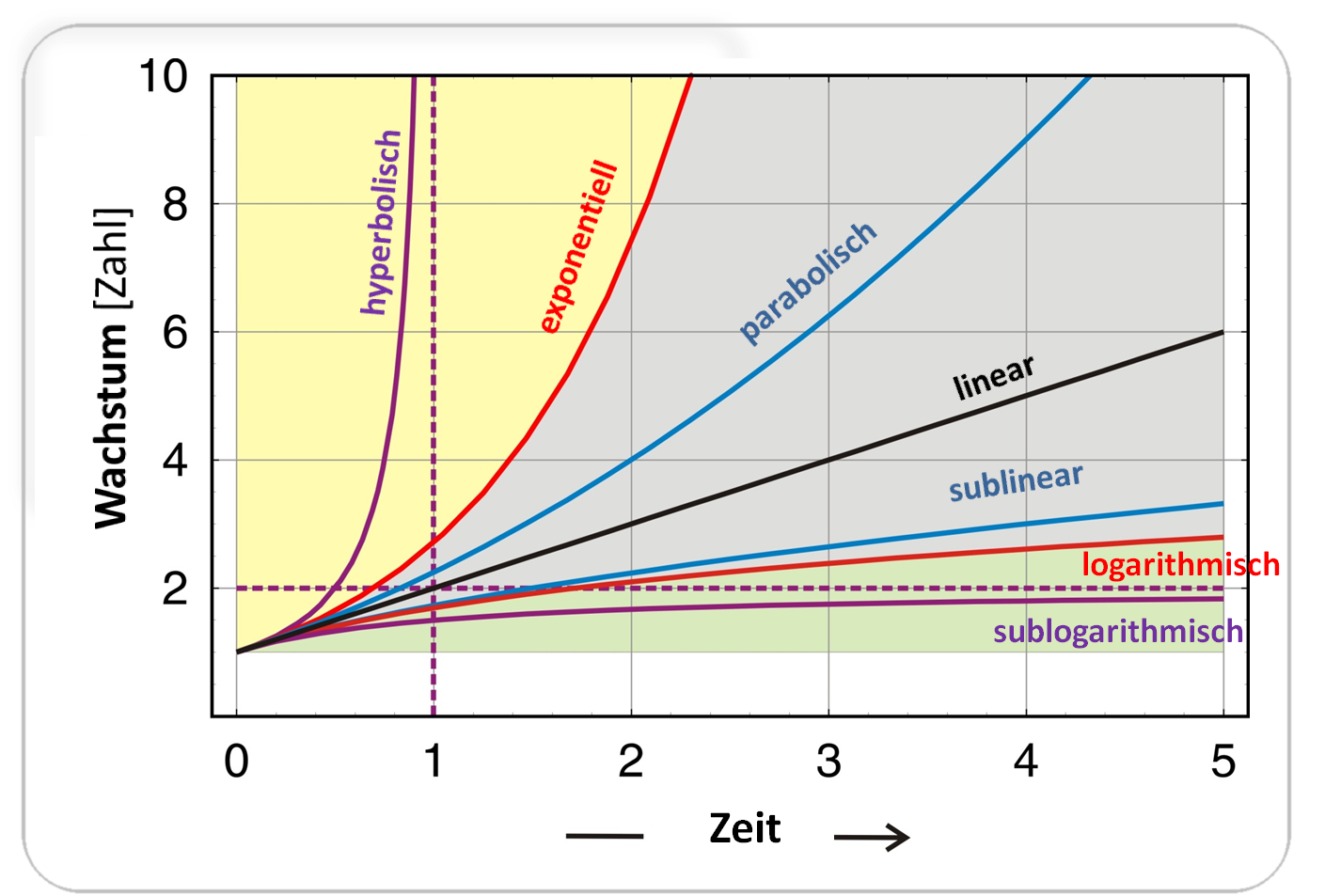 Abbildung 2. Grenzenloses Wachstum – Idealisierte Funktionen. Zu Beginn (Zeitpunkt: 0) haben alle Funktionen den Wert: x(0) = 1. Wachstum: i) hyperbolisch ( x(t) = 1 / (1-t) ; lila) ii) exponentiell (x(t) = expt; rot) iii) parabolisch (x(t)=(1+t/2)²; blau), iv) linear (x(t) = 1 + t; schwarz), v) sublinear (x(t) = 1+t/(1+t); blau), vi) logarithmisch (x(t) = 1+log(1+t); rot), sublogarithmisch (x(t) = 1+t/(1+t); lila). Im gelben Bereich erreicht das Wachstum den Wert „unendlich“ in endlicher Zeit, im grauen Bereich dagegen erst nach unendlicher Zeit und es bleibt endlich Im grünen Bereich auch nach unendlicher Zeitdauer.
Abbildung 2. Grenzenloses Wachstum – Idealisierte Funktionen. Zu Beginn (Zeitpunkt: 0) haben alle Funktionen den Wert: x(0) = 1. Wachstum: i) hyperbolisch ( x(t) = 1 / (1-t) ; lila) ii) exponentiell (x(t) = expt; rot) iii) parabolisch (x(t)=(1+t/2)²; blau), iv) linear (x(t) = 1 + t; schwarz), v) sublinear (x(t) = 1+t/(1+t); blau), vi) logarithmisch (x(t) = 1+log(1+t); rot), sublogarithmisch (x(t) = 1+t/(1+t); lila). Im gelben Bereich erreicht das Wachstum den Wert „unendlich“ in endlicher Zeit, im grauen Bereich dagegen erst nach unendlicher Zeit und es bleibt endlich Im grünen Bereich auch nach unendlicher Zeitdauer.
Hyperbolisches, exponentielles und parabolisches Wachstum verbrauchen sehr rasch und effizient die vorhandenen Ressourcen. Dementsprechend liegt die einzige Möglichkeit mit raschem Wachstum zurecht zu kommen in der Wiederverwertung - dem Recyceln – von Material: stärkeres Wachstum von Varianten mit begrenzter Lebensdauer führt zu einer erhöhten Absterberate und damit zu mehr an recycelbarer Substanz. Auch lineares Wachstum und das noch langsamere logarithmische Wachstum nähern sich der Unendlichmarke, wenn man unendlich lang wartet.
In allen diesen Fällen ist Recycling also eine Voraussetzung für effizientes Wachstum aber keine ausreichende Bedingung – es können ja Ressourcen, wie beispielsweise Energie, dabei (vollständig) aufgebraucht werden.
Nur die langsamste „sublogarithmische“ Form erreicht auch nach unendlich langer Zeit einen endlichen Grenzwert. Es erscheint wichtig darauf hinzuweisen, daß nur diese langsamste Form des Wachstums mit einem Reservoir an vorhandenen Ressourcen auskommen und über längere Zeit aufrechterhalten werden kann. Dieser Typ Wachstumskurve zeichnet sich dadurch aus, dass die Wachstumsraten mit zunehmender Dauer sinken.
Jede Form grenzenlosen Wachstums – charakterisiert durch Wachstumskurven mit hyperbolischem, exponentiellem, parabolischem, linearen und sublinearem Verlauf – kann nur für begrenzte Zeitdauer andauern. Es muß hier nicht besonders betont werden, daß Ökonomen, die eine konstante Wachstumsrate predigen, in der einen oder anderen Weise einem Trugschluß unterliegen.
Recycling ist ausreichend um Darwinsche Selektion in einer konstant bleibenden Population fortbestehen zu lassen und Grenzen der Populationsgröße können prinzipiell für alle Formen des Wachstums erzwungen werden – Recyceln der Ressourcen hilft dann die Populationen zu erhalten.
Ursprung des Lebens – Autokatalyse - Recycling
Theoretische und experimentelle Modelle zum Ursprung des Lebens konzentrieren sich üblicherweise auf ein oder mehrere der drei Kernpunkte, nämlich auf die
i. Erzeugung, Speicherung und Erhaltung von Information in den Genen,
ii. Aufnahme von Energie und Umwandlung zur Treibkraft von Stoffwechselprozessen,
iii. Schaffung eines abgeschlossenen lokalen Umfelds durch Kompartimentbildung
Basis der Darwin’schen Selektion und unabdingbar auch in den frühesten Phasen der Evolution - im Übergang von unbelebter zu lebender Materie - ist dann der autokatalytische Prozeß, der zur Vervielfachung der Spezies führt (s.o.). Der noch präbiotische Stoffwechsel muß die zentrale Hauptaufgabe lösen: die Produktion der Bausteine, aus denen die wichtigsten Biomoleküle, Proteine und Nukleinsäuren, hergestellt werden können - ein riesiges Reservoir an organischen Verbindungen in ein relativ kleines Set von Schlüsselmolekülen zu „kanalisieren“.
In die Diskussion, wie ein derartiger früher Stoffwechsel ausgesehen haben könnte, ist erst in jüngster Zeit auch der Aspekt des Recycelns eingeflossen. Es bedeutet zweifellos einen Selektions-Vorteil, wenn in der Reaktion A + X → 2X das autokatalytische Produkt X zu einem weiteren Produkt D abgebaut wird, das in einem Energie-abhängigen Prozess wieder in den Ausgangsstoff A zurückverwandelt – recycelt - werden kann. Ein derartiges Recycling-System, das seine Energie aus photochemischen Reaktionen beziehen sollte, wurde bereits vor drei Jahrzehnten vorgeschlagen [2]. Interessanterweise bezieht die erste, mit eigenem Stoffwechsel ausgestattete Protozelle (das „Los Alamos Bug“) ihre Energie aus einer photochemischen Reaktion an einem Rutheniumkomplex.
Offensichtlich ist Photochemie die geeignetste Taktik um energieabhängige Reaktionen zu ermöglichen: Licht als Energiequelle erscheint ja unerschöpflich. Lichtabhängige an Membranen gekoppelte Reaktionen dürften auch die ersten und bis jetzt effizientesten Wege gewesen sein, auf welchen präbiotische und frühe prokaryotische Zellen Energie „einfingen“ und in chemische Energie umwandelten [3]: Die ältesten uns bekannten Fossilien sind vermutlich Relikte ursprünglicher photosynthetischer Cyanobakterien [4]. Dazu kommt, daß photochemische Reaktionen hochspezifisch ablaufen und zu hohen Produktmengen führen können, vor allem, wenn die Quantenausbeute keine Rolle spielt.
Bevölkerungswachstum und Recycling
Kommen wir nun wieder auf unser ursprüngliches Problem zurück – die Ernährung einer exponentiell wachsenden Weltbevölkerung (Abbildung 3).
Malthus, dessen Prognosen offensichtlich nicht eintrafen, konnte natürlich den technischen Fortschritt im vergangenen Jahrhundert, insbesondere die „Grüne Revolution“ nicht voraussehen. Auf Grund der Verwendung von modifizierten Pflanzen, synthetisch hergestellten Düngemitteln, Pestiziden, Bewässerungssystemen und der Mechanisierung der Feldarbeit sind die Ernteerträge weltweit enorm gestiegen und haben trotz der enorm gestiegenen Population den „Hunger in der Welt“ reduziert (aber nicht beseitigen können).
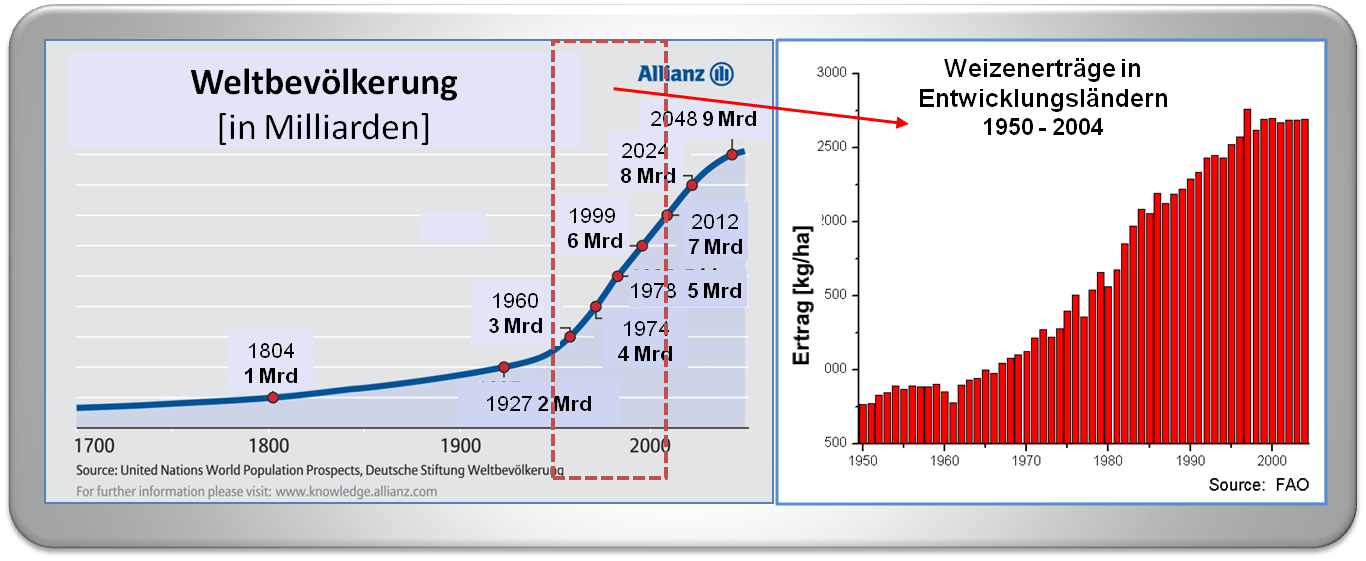 Abbildung 3. Innerhalb der letzten 60 Jahre ist die Weltbevölkerung nahezu auf das Dreifache angewachsen. Gleichzeitig führte die „Grüne Revolution“ zur enormen Steigerung der Ernteerträge.
Abbildung 3. Innerhalb der letzten 60 Jahre ist die Weltbevölkerung nahezu auf das Dreifache angewachsen. Gleichzeitig führte die „Grüne Revolution“ zur enormen Steigerung der Ernteerträge.
Die Grundprobleme bestehen aber weiter. Das Bevölkerungswachstum setzt sich ungebrochen fort, die landwirtschaftliche Produktion verlangsamt sich, es gibt nur wenige neue, für den Ackerbau geeignete Gebiete, die Verstädterung reduziert zusätzlich landwirtschaftlich nutzbare Flächen. Dazu kommen alle die durch die Intensivwirtschaft verursachten negativen Effekte auf die Umwelt.
Damit stellt sich die Frage, inwieweit Ressourcen/Rohstoffe langfristig zur Verfügung stehen werden und wie diese aus industriellen Abfällen wiedergewonnen werden können.
Wertvolle Metalle lassen sich leicht recyceln, die meisten Metall erzeugenden Konzerne besitzen ein Repertoire an Verfahren, um jegliche Art von Metall aus Rückständen und Schlacken aufzureinigen, und sie wenden diese Verfahren an, wann immer die Preise auf dem Weltmarkt genug hoch sind.
Hinsichtlich der landwirtschaftlichen Nutzung sind Verbrauch und Recycling zweier essentieller Elemente zu beachten, die eine conditio sine qua non für jegliches Leben darstellen: Stickstoff und Phosphor.
Recycling von Stickstoff
Gasförmiger molekularer Stickstoff (N2) ist ubiquitär, findet sich in unerschöpflichen Mengen in in unserer Atmosphäre. Allerdings kann Stickstoff in dieser Form weder von Pflanzen noch von Tieren verwertet werden, nur einige Bakterienstämme sind dazu in der Lage und produzieren daraus Stickstoff-haltige Moleküle, zum Nutzen aller anderer Organismen.
Bis zum Beginn des 20. Jahrhunderts gab es nur zwei Formen von Techniken zur Gewinnung eines für uns verwertbaren Stickstoffs, durch Verwendung von: i) Leguminosen – d.i. Hülsenfrüchte –, die in Symbiose mit den Stickstoff-assimilierenden Bakterien der Spezies Rhizobium leben, und ii) Dünger aus Guano, dem Exkrement von Vögeln, welche auch heute noch in großen Kolonien die Inseln entlang der Küste von Peru und Chile besiedeln. Die Verwendung von Guano als Dünger bedeutet ein Recyceln des Stickstoffs, allerdings mit einer unglaublich langen Zykluszeit.
Diese Situation änderte sich vollkommen, als zwei deutsche Chemiker, Fritz Haber und Carl Bosch, ein Verfahren erfanden, in welchem sie aus molekularem Stickstoff und Wasserstoff mit Hilfe eines Katalysators Ammoniak herstellen konnten. Auch, wenn dieses Verfahren äusserst viel Energie verbraucht, haben die aus dem synthetischen Ammoniak hergestellten Düngemittel den natürlichen Guanodünger praktisch vollständig ersetzt – vermutlich war dies die wichtigste Grundlage einer ausreichernden Nahrungsmittelproduktion für eine enorm gewachsene und weiter wachsende Weltbevölkerung. Die Relevanz der Ammoniaksynthese ist vielleicht am besten aus einer Abschätzung von Robert Horwath aus dem Jahr 2008 ersichtlich: dieser findet, dass bereits mehr als 80 % des in den menschlichen Proteinen eingebauten Stickstoffs eine Haber-Bosch Anlage von innen gesehen haben.
Der Stickstoff-Zyklus ist ein hervorragendes Beispiel für ein Recycling mit einem riesigen Reservoir. Die Produktion von synthetischem, verwertbarem Stickstoff stößt praktisch an keine Grenzen außer an die der Energieversorgung und der Umweltprobleme auf Grund der intensivst betriebenen Landwirtschaft und der durch Düngemittel verursachten Verunreinigung von Wasser.
Recycling von Phosphor
Phosphor ist ein essentielles Element in unseren Biopolymeren, beispielsweise den Nukleinsäuren. Intensiver Ackerbau benötigt Phosphat-haltigen Dünger, darüber hinaus sind Phosphate unabdingbare Bestandteile moderner Waschmittel.
Die herkömmliche Quelle für Phosphor sind phosphatreiche Mineralien (z.B. Apatit). Frühere Lagerstätten sind nun aber bereits weitgehend erschöpft, geeignete neue, mit geringer (Schwermetall-) Verunreinigung zunehmend schwerer zu finden. In Analogie zu dem häufig verwendeten Begriff „peak oil“ – also dem Ende des Erdöls - sprechen einige Experten schon vom „peak phosphorous“.
Mittlerweile hat die Phosphor-Industrie Strategien entwickelt um Phosphate aus Abwässern zurückzugewinnen. Hier besteht aber ein gravierender Unterschied zum Recyceln von Stickstoff, der in reiner Form aus einem praktisch unerschöpflichen Reservoir erhalten wird: Die Rückgewinnung von Phosphaten erfolgt aus hochverdünnten Lösungen, die jede Menge Verunreinigungen enthalten, eine Aufreinigung von Phosphaten, die bereits in Flüsse oder gar ins Meer gelangt sind, ist ökonomisch praktisch nicht vertretbar.
Fazit
Exponentielles Wachstum erschöpft alle Reservoire an Ressourcen. Ist ein essentielles Reservoir entleert und eine Auffüllung nicht möglich, so stirbt die Mangel leidende Population aus. (Experimentelle Modelle zur präbiotischen Evolution haben hier ihre Schwachstellen.)
Recyceln bietet eine Lösung des Problems, da die Menge des recycelten Materials mit der Menge an Autokatalysatoren gekoppelt ist und die Effizienz des Recyclingprozesses, zusammen mit anderen Faktoren, die Menge an Autokatalysatoren bestimmt, die aufrechterhalten werden kann. Dies gilt in gleicher Weise für die früheste („primordial“) Form der Autokatalyse, für die biologische Evolution der Spezies und ebenso für die Entwicklung der menschlichen Gesellschaften.
[1] Robert Malthus: Eine Abhandlung über das Bevölkerungsgesetz oder eine Untersuchung seiner Bedeutung für die menschliche Wohlfahrt in Vergangenheit und Zukunft, nebst einer Prüfung unserer Aussichten auf eine künftige Beseitigung oder Linderung der Übel, die es verursacht (6. Auflage, aus dem Englischen übersetzt und frei abrufbar; Digitale Texte der Bibliothek des Seminars für Wirtschafts- und Sozialgeschichte, Uni Köln) http://www.digitalis.uni-koeln.de/Malthus/malthus_index.html
[2] Schuster, P.; Sigmund, K. Dynamics of evolutionary optimization. Ber. Bunseges. Phys. Chem. 1985, 89, 668-682.
[3] Lane, N.; Martin, W.F. The origin of membrane bioenergetics. Cell 2012, 151, 1406-1416.
[4] Schopf, J.W. Fossil evidence of Archaean life. Phil.Trans.Roy.Soc.London B 2006, 361, 869-855.
Eine ausführlichere Version dieses Essays (in Englisch) findet sich auf der homepage des Autors: http://www.tbi.univie.ac.at/~pks/Preprints/pks_365.pdf
*Glossar
Autokatalyse: Das Produkt (X) einer Reaktion ist ein Katalysator, der von ihm selbst katalysierten Reaktion: (A) + X → 2X. Da im Verlauf der Reaktion das Produkt - die Menge des Katalysators - ansteigt, nimmt die Geschwindigkeit der Reaktion exponentiell zu.
Arithmetische Progression: Zahlenfolge, in der aufeinanderfolgende Zahlen sich um denselben Betrag erhöhen, z.B. um 1: 1, 2, 3, 4, 5, 6,…..
Geometrische Progression: Zahlenfolge, in der aufeinanderfolgende Zahlen in einem konstanten Verhältnis stehen, also mit demselben Faktor multipliziert werden; z.B. mit dem Faktor 2: 2, 4, 8, 16, 32, 64,….
Exponentialfunktion: In gleich langen Zeitintervallen ändert sich der Funktionswert um denselben Faktor: y = aX (a: Basis, x: Exponent), beispielsweise beträgt bei einer Basis 2 der Funktionswert nach 1, 2, 3, 4, 5, 6 Zeitintervallen: 21, 22, 23, 24, 25, 26,………also: 2, 4, 8, 16, 32, 64,….Der Verlauf natürlicher Prozesse des Wachstums und auch des Zerfalls (z.B. des radioaktiven Zerfalls) wird am besten durch eine Funktion mit der sogenannten natürlichen Basis e, der von Leonhard Euler eingeführten Zahl = 2,7182….dargestellt, also f(x) = ex.
Weiterführende Links
Nur noch Stehplätze. Thomas Robert Malthus: Das Bevölkerungsgesetz (Christoph Neßhöver 1999, Zeit online) http://www.zeit.de/1999/21/199921.biblio-serie_.xml
Bevölkerungswachstum: Die Welt ist nicht genug (M. Becker, Spiegel Online 2011). http://www.spiegel.de/wissenschaft/mensch/bevoelkerungswachstum-die-welt-ist-nicht-genug-a-794203.html